What is an Exponential Function?
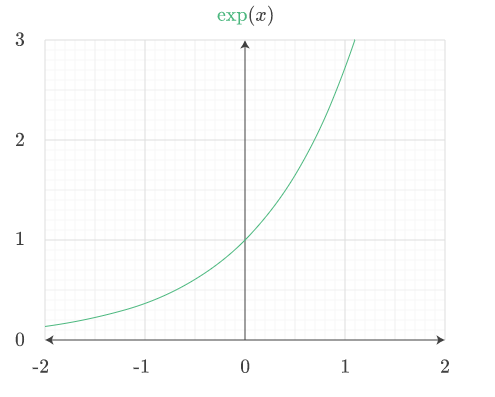
As the name suggests, the exponential function consists of exponents. An exponential function has a constant as its base as well as a variable as the exponent. Besides, if a function has a variable as its base and a constant as the exponent, then it is known as a power function, and not an exponential function. In the terms of mathematics, we see, an exponential function is a function of form f(x)=ax, where x=a variable and a is the constant which is also the base of the function f(x) and the value of a should be greater than 0.
Forms of an Exponential Function
A famous exponential function is f(x)=ex, given that e is Euler’s number and its value is 2.718… By considering the possibilities of all the exponential functions, we can see that one of such functions can have a constant as the multiple of the variable put as the power. Therefore, the expression of the function can look like- f(x)=ekx. Besides, it can also look in the form of f(x)=pekx, provided that p is constant. Therefore, the different forms of an exponential function are as follows:
- f(x)=bx
- f(x)=abx
- f(x)=abcx
- f(x)=ex
- f(x)=ekx
- f(x)=pekx
Given that b>0 and b≠1.
In the above expressions, except ‘x’, all other letters are constants, x is the variable and the exponential function is expressed as f(x) in terms of x. Also, note that the base in every exponential function is a positive number, which means, b>0 and e>0. ‘b’ must not be equal to 1.
There are some differences between exponential growth and exponential decay, one of them is that in exponential growth, quantity increases slowly at first and then rapidly, whereas, in exponential decay, the quantity decreases very quickly at first and then slowly.
Exponential Series
The real exponential function can usually be defined in the following power series,
- ex =∑∞n=0∑n=0∞xn/n!=(1/1)+(x/1)+(x2/2)+(x3/6)+….
An extension of some of the other exponential functions are given below:
- e=∑∞n=0∑n=0∞ xn/n!=(1/1)+(1/1)+(1/2)+(1/6)+….
- e-1=∑∞n=0∑n=0∞xn/n!=(1/1)-(1/1)+(1/2)-(1/6)+….
Rules of an Exponential Function
The rules of an exponential function are similar to that of the rules of exponents. The following is the list of such rules:
- Law of Zero Exponent: a0=1
- Product Law: am×an=am+n
- Law of Quotient: am/an=am-n
- Law of Power of a Power: (am)n=amn
- Law of Power of a Product: (ab)m=ambm
- Law of Power of a Quotient: (a/b)m=am/bm
- Law of Negative Exponent: a-m=1/am
Equality Property of an Exponential Function
As per the equality property of an exponential function, if there are two exponential functions whose bases are the same, then the exponents of those functions would also be the same.
Exponential Function Derivative
The following are the differentiation formulas used to find the derivative of the exponential function:
- d/dx (ex) = ex
- d/dx (ax) = ax ln a.
Integration of Exponential Function
Apart from the above ones, here are some formulas from integration that we use to find the integral of the exponential function:
- ∫exdx=ex+C
- ∫axdx=ax/(ln a)+C
Online Math Classes
In today’s generation, especially after the Covid-19 outbreak, online courses have come to the rescue. From kindergarteners to office workers – everyone is now dependent on the Internet. Students conduct their classes online. It becomes more interesting when they have access to websites that offer various articles on learning materials. However, we generally see students avoiding math when they sit down to study. One reason may be that the foundation of knowledge in mathematics is not strong enough. This is where Cuemath supports students. They offer online math classes that help students understand topics better, have fun, and review formulas and calculation examples.
To learn more about exponential function in a fun and better way, visit Cuemath.